Signal to noise ratio

Signal and Noise #

We took several long exposure frames and stacked them to reduce noise in our Deep Space images. We do long exposures because we want to get more photons, because we want to increase our signal. We stack frames not to add their light, but to average their noise.

When we detect light, the number of photons we detect is not constant for a fixed level of brightness. They fluctuate randomly around the real value. We call this fluctuation shot noise. It is important to note that this noise is not introduced by the equipment. This shot noise is proportional to the square root of the signal, so higher signal level has more shot noise than lower levels.

This shot noise is to blame for the imperfections in dark signal removal. The dark signal is caused by thermal photons coming from the environment and the electronics in your camera. They expose your detector as the real photons from the source. We use a dark frame subtraction operation to try to remove them. When you stack your dark frames, you are averaging the dark signal in each pixel to an average dark value for this pixel. But in each light frame, the dark signal is also affected by its own shot noise, so it will never completely eliminate the noise produced by the dark signal.

As we have seen before, the noise is proportional to the $\sqrt{(\text{value})}$ , so the only way to reduce its effect is by reducing the level of the dark signal. To do that, we use cooled cameras or very short exposure times. Cooled cameras have fewer thermal photons detected by the detector. Short exposures allow fewer photons to reach each frame, so we have a lower dark signal that is more stable and easier to eliminate completely.

Lucky Imaging #

So if you have a cooled camera, you can keep lowering the temperature and shoot long exposures to capture your subjects. But if your camera is not cooled or its tracking is not good enough for taking long exposures, you can try reducing the noise by taking short exposures. Yes, I know, it seems counterintuitive, but for certain types of cameras it works. This is related to another noise source that I have ignored so far, the read noise. This noise is related to the conversion of photons, trapped as electrons by the detector into a signal transferred to your computer. A lot of electronics are involved in this process, but it is characterized by a single figure: the reading noise, usually expressed in electrons / px.

On classic CCD cameras this read noise was around 6 or 7e / px. And remember this error is signal independent, so if your exposure wasn’t long enough to accumulate more than 7 signal electrons, you will be hopelessly lost on this floor of read noise. This is why you need long single exposures to detect weak sources when using these cameras.

Fast forward for three decades. Today, the most widely used detectors for astrophotography are CMOS, not CCD. These detectors have very different electronics and detector designs. This changes many things. The one that interests us is the reading noise. CMOS cameras have very low levels of read noise. In fact, the cameras we use for planetary photography tend to have read noise very close to or less than 1e / px.

At this level of read noise, taking 1x120s frames or stacking 12x10s frames is almost the same, because the process of reading each individual frame does not add a significant amount of noise. You can see a long explanation from the author of the SharpCap software, Dr. Robin Glover, at this talk

So our plan is to take hundreds or thousands of short exposure images and stack them to get a clean image. It works great, last December I used a QHY5III462C camera to take 740x10s images of M1 with a 85mm refractor and stack them, as you can see the 2 hour equivalent exposure allows me to extract a lot of fine details:

Seeing the signal emerge from the noise #

The end result is fine, but I want to see how this image can emerge from my 10s shots. Because if I show you one of them, you will NOT believe that this final image comes from these individual frames. Let’s see one of them chosen at random:

This frame is already stretched, so you can see some stars, but the nebula is an amorphous blob in the middle of the cropped frame.

One cool thing about this shot noise: our brain/eye system knows how to handle it. Partially. Every time you see a movie (video), your brain / eyes are playing the same trick. It’s what we call persistence of vision , basically your visual system is stacking and averaging continuously by some fractions of a second. If you are presented with a short burst of individual images, your brain doesn’t see them one by one but as a composed image. If there are some displacements between frames, we see movement.

In our case, if we compose all the raw (stretched) frames as a video and play them back at 24 fps, your brain will “average” the shot noise and you can see through the noise veil. In this video, you can see how faint stars appear through the haze and how the nebula in the middle of the frame is best defined.

So what I wanted is to see how the final image comes out of this sea of noise and this is where Siril’s scripting capabilities come in.

But before we begin the stacking process, we need to perform some basic processing. The calibration and register steps will be the same over an over again. So, the first phase of this adventure will be to run the OSC_Preprocess script to generate the r_pp_light sequence perfectly calibrated and aligned, ready to be stacked. In fact, as I’ve been using an OSC and I can’t colour balance each frame individualy, I’ve choosen to extract the synthetic Halpha channel using the script OSC_Extract_Ha instead. This will produce a more treatable monochrome set of images. I’ve also used the GUI to crop a 1000x1000 subimage centered around the nebula. After having renamed them to org_xxxxx.fits, we can start with the stacking.

My plan was to make 740 stacks. The first will not be a stack, but a single frame. The second stack will contain only frames 1 and 2, the third stack will contain frames 1, 2 and 3 and so on until you reach stack 740 which will contain all the frames. This last one will be the standard stack that we perform in a regular session.

Obviously, producing 740 stacks by hand, with different frames on each, was a daunting mission. So I started thinking about scripts. I know Siril scripts are limited - we don’t have variables, we don’t have control flow statments. But Siril is not alone. In a good Unix tradition, Siril isn’t just a fancy GUI app where you can use your mouse to tap. It is also a command line tool that can be started to run a task and exit. And this task could be a Siril script.

So my plan was to use some bash scripts to coordinate the whole process and do the cleanup and a very simple Siril script to stack. I have put all the stacked images in a folder called anim. Here I have the frames org_00001.fits, org_00002.fits … org_00739.fits. We will iterate 739 times and in each loop I will copy an image to a folder called process. Then I’ll start Siril with a custom script to stack the images in the process folder. After Siril produces its output, I’ll copy the stacked image into a new stacked folder with the same name as the newly added image. The initial state will be:

At the end of the process I’ll have the stacked folder populated with the sequence org_00001.fits, org_00002.fits … org_00739.fits, but this time on this sequence, each frame will be an incremental stack.

I will show you the Siril script first. You will be disappointed, it’s so simple:

requires 0.99.4

cd process
stack org rej 3 3 -norm=addscale -output_norm
cd ..

Enter process folder, stack the org files and step out. One task. Simple.

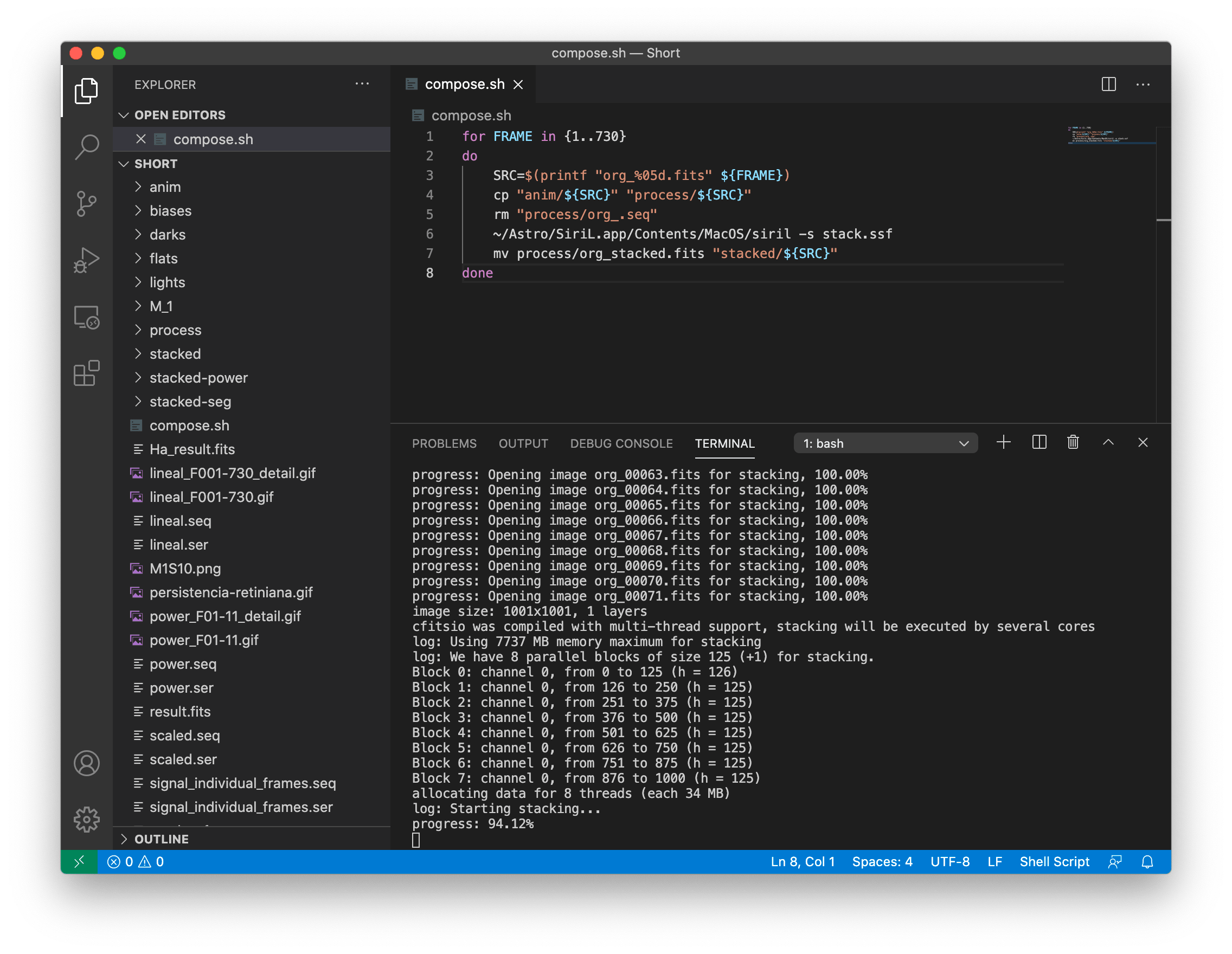
Then I will show you the bash script that runs the show:

for FRAME in {1..730}
do
	SRC=$(printf "org_%05d.fits" ${FRAME})
	cp "anim/${SRC}" "process/${SRC}"
	rm "process/org_.seq"
	~/Astro/SiriL.app/Contents/MacOS/siril-cli -s stack.ssf
	mv process/org_stacked.fits "stacked/${SRC}"
done

As you can see, there is nothing too complicated in this file either. Iterate over frame number, create the frame filename, copy it and launch Siril. After the stack has finished, store the new stack with the current frame name. Since I am running this whole process on a macOS computer, the way I need to invoke Siril is a bit weird, but in the end I’m just running Siril with the -s switch and the script name.

As we are reusing the same process folder each run, it is important to delete the previously created .seq file or Siril will not look for the newly added frames.

And that’s it, run this script and relax, because it will take a while to generate all the frames for our animation.

Out of the Sea of Noise #

After the process is complete, I open the Siril GUI as usual, select the stacked folder as my working folder, search for sequences and transform the one found into a SER file. You can open this video in SER Player to see the image emerging from the Sea of Noise :). I have exported the video to mp4 format, so you can see it on this page:

As you can see, the image improves frame by frame as you add more components to the stack. Not only does the contrast increase and the background noise level recedes, but you can see fine details emerge in the nebula as the shot noise is averaged more and more and the true signal can be observed.

At first the enhancements are more apparent and then the enhancement rate starts to slow down. You may be wondering how many images should you stack?

As much as you can. The signal-to-noise ratio always improves when you add more images. The problem is that the ratio of enhancements is not linear with the number of images stacked.

In general, the signal-to-noise ratio for stacks depends on $\sqrt{(\text{N})}$ where N is the number of frames stacked. If you look at the graph of $\sqrt{(\text{N})}$, you will see that the slope becomes less pronounced as N increases, so the number of frames you need to add increases with the number of frames already stacked.

For example, I extracted the stack labeled 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, and 730 (the latter should be 1024, but I don’t have that many frames!). Each stack has twice as many frames as the previous one. So if we look at the signal-to-noise ratio, we find that the ratio for the N-frame stack is

So, in this sequence, each frame has a signal-to-noise ratio 1.41 times better than the previous one. We hope to see a steady improvement in image quality. And in fact this is what you can see in the two following animations.

Conclusion #

Siril isn’t just a beautiful tool for producing stunning images. It could be a useful tool that integrates into broader toolchains that integrate multiple tools.

And remember if you have N images and you want to significantly improve the quality, don’t think about adding images, think about doubling the number.